Examens de Microéconomie S2-L1 avec correction

 

Licence d’Economie et Gestion -Première année Groupes 2 et 5

Durée : 45 minutes

Questions de cours (4 points)

1. Définissez la notion d’élasticité prix directe de la demande d’un bien (formule de calcul, interprétation, types de biens en fonction de ses valeurs). (2 points)

Réponse :

L’élasticité prix directe de la demande d’un bien est le rapport entre la variation relative de la consommation de ce bien à la variation relative du prix du bien. (0,75 points)

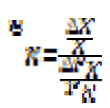
- mesure le pourcentage de variation de la consommation du bien X qui résulte d’une augmentation de 1% du prix de ce bien (0,75 points)

Types de biens : l’élasticité prix est négative, hormis le cas peu probable du paradoxe de Giffen. Donc si l’élasticité prix directe est négative, nous avons des biens normaux, typiques. Si l’élasticité prix directe est positive nous avons des biens atypiques. (0,50 points)

2. Définissez les économies d’échelle et les déséconomies d’échelle. (2 points) Réponse :

Une entreprise fait des économies d’échelle quand elle peut doubler sa production en faisant moins que doubler les coûts. (1 point)

Il y a déseconomies d’échelle lorsqu’un doublement de la production fait plus que doubler les coûts. (1 point)

 

Exercices (16 points)

• Une entreprise a pour fonction de production . 

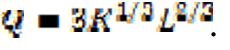
1. Lorsque l’entreprise augmente la quantité de capital employée, la productivité marginale du capital est-elle croissante, décroissante, constante ? (5 points)

Réponse :

• La productivité marginale du facteur capital   (2 points)

• Pour déterminer si la productivité marginale du capital est croissante, décroissante ou constante, on la dérive par rapport au capital : (1 point)

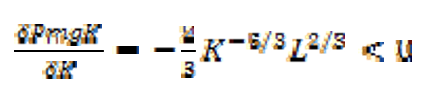
  (1,5 points)

Il résulte que la productivité marginale du capital est décroissante. (0,5 points)

1. Définissez le TMST du travail au capital et établissez sont expression dans le cas de la fonction de production donnée. Si on pose L=6 et K=3, quelle sera sa valeur ? (5 points)

Réponse :

• Le TLMT du travail au capital représente la réduction de la quantité d’input de capital permettant de maintenir constant le niveau de production lorsqu’une unité supplémentaire de travail est utilisée. (2 points)

(1,5 points)

• Dans notre cas :       

(1 point)

• Si l’on pose L=6 et K=3,

(0,50 points)

c. On sait que l’équation de coût total est donnée par l’expression :

Supposons que le prix du capital r=6 et le prix du travail w=10. Le coût total este C=90. Détermines les valeurs optimales des facteurs de production et le coût associé. Déterminez et définissez le sentier d’expansion(en donner l’équation de la forme K=f(L)).  (6 points)

Réponse :

• Le programme du producteur s’écrit :

Le Lagrangien prend la forme suivante : (2 points)

Les conditions de premier ordre :  (0,5 points)

Il résulte que

et donc   

                    

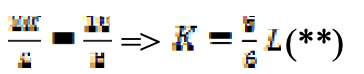
(0,5 points)

Nous replaçons la relation (**) dans l’équation d’isocoût et nous obtenons :

donc L*=6 et K*=5    (0,8 points)

Le coût associé est C*=10L*+6K*=60+30=90   (0,2 points)

• Le sentier d’expansion représente l’ensemble des combinaisons de facteurs correspondants au moindre coût, pour les différents niveaux de production. (1 point)
• Nous avons déjà déterminé le sentier d’expansion ; c’est la relation entre les facteurs K et L trouvé à partir des 2 premières conditions de 1^er ordre du Lagrangien.  (1 point)