La statistique descriptive est un module pratique étudié au semestre 1 visé à former les étudiants de semestre 1 afin d'avoir les astuces et les bases pour résoudre et analyser les données d'une manière exacte et efficience, le module de statistique descriptive S1 contient plusieurs différents axes chaque axe traiter une partie après avoir maîtrisé les informations vous êtes obligés de faire des exercices, alors cet article vise à donner et propose des exercices de statistique descriptive S1 pour s'entraîner et tester tous les connaissances collectées au cours de statistique descriptive S1, les exercices visent à fixer les informations et s'entraîner en même temps en vue que le module de statistique descriptive est un module pratique, si vous avez trouvé des difficultés au niveau des informations vous pouvez voir soit le cours soit le résumé qui contient les informations les plus importantes vues au module de statistique descriptive S1.
Statistique descriptive S1 - Licence 1 Semestre 1 : Exercices avec corrigés
Les exercices de statistique descriptive S1 peuvent se différencier d'un professeur à autre mais en général restant les mêmes sauf des petites différences, les exercices que vous allez trouver dans cet article sont diverses chaque exercice traîter une partie étudiée au cours de statistique descriptive S1, les exercices de statistique descriptive S1 suivent la même astuce et les mêmes étapes afin de résoudre des problèmes alors il suffit de faire plusieurs exercices afin de fixer et maîtriser les étapes suivies à répondre aux questions liées au statistiques descriptives.
Les exercices de statistique descriptive S1 ont pour but de faire pratiquer tous les informations et les relations économiques et mathématiques vues au cours de statistique descriptive afin de savoir comment on peut utiliser les relations économiques et mathématiques pour répondre aux exercices et résoudre des problèmes en relation avec la statistique descriptive S1, sans oublier quelques définitions.
Les exercices de statistique descriptive S1 son but est de faciliter la préparation mais quelles sont les étapes à suivre pour répondre d'une manière exacte aux exercices de statistique descriptive S1 ? Comment on peut répondre d'une manière exacte et correcte ? Quelles sont les relations mathématiques et économiques les plus importantes utilisées au statistique descriptive S1 ? à quoi servent les exercices de statistique descriptive S1 ? Si on a trouvé des difficultés à répondre aux quelques questions comment on peut arriver à trouver la solution ?
Quelles sont les étapes à suivre pour répondre d'une manière exacte aux exercices de statistique descriptive S1 ?
Les étapes à suivre pour répondre aux exercices restant les mêmes donc il suffit de faire pas mal des exercices afin de savoir et maîtriser les étapes suivies pour répondre aux exercices.
Comment on peut répondre d'une manière exacte et correcte ?
Pour répondre d'une manière exacte et correcte il faut d'aboord savoir et maîtriser la relation à utiliser pour résoudre le problème.
Quelles sont les relations mathématiques et économiques les plus importantes utilisées aux statistiques descriptives S1 ?
On ne peut pas dire que cette relation est plus importante que cette relation, toutes les relations étudiées et traitées au cours de statistique descriptive S1 sont importantes donc on peut ne pas faire une différenciation entre les relations économiques et mathématiques vues au module.
Si on a trouvé des difficultés à répondre aux quelques questions comment on peut arriver à trouver la solution ?
Lorsqu'on trouve des difficultés à répondre aux exercices de statistique descriptive S1 il suffit de savoir quel est la partie qu'on doit maîtriser au cours pour répondre à cette question après on peut faire une autre préparation afin de dépasser cette difficulté.
Support
Le support de exercices statistique descriptive S1 vise à fixer les informations collectées au module de statistique descriptive S1, le support contient plusieurs différents exercices chaque exercice traîter une partie vue au cours de statistique descriptive S1, si vous avez trouvé des difficultés ou vous avez besoin à des informations vous pouvez mentionner les dans un commentaire ou nous contacter sur la page nous contacter.
TD n°1
Exercice n°1.
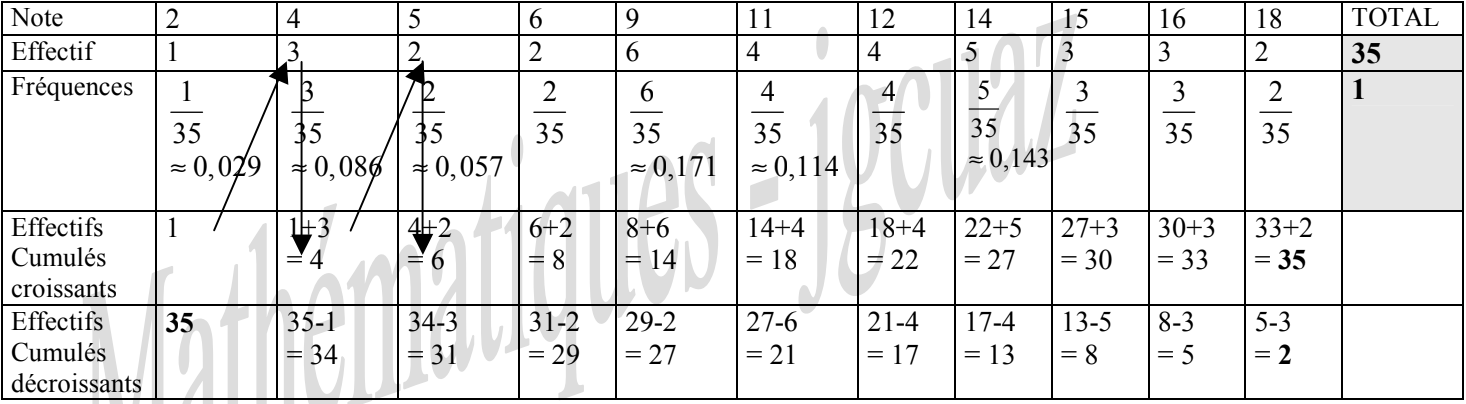
Les 35 élèves d'une classe ont composé et le tableau ci-dessous donne la répartition des diverses notes.
Recopier et compléter ce tableau en calculant les fréquences à 10-3 près, et les effectifs cumulés croissants et décroissants.

Exercice n°2.
Un établissement de transfusion sanguine a dressé le bilan de sa collecte de sang pendant un an
| Age du donneur | % Correspondant |
| Moins de 20 ans | 4% |
| Entre 20 et 29 ans | 14% |
| Entre 30 et 39 ans | 24% |
| Entre 40 et 49 ans | 32% |
| Plus de 50 ans | 26 |
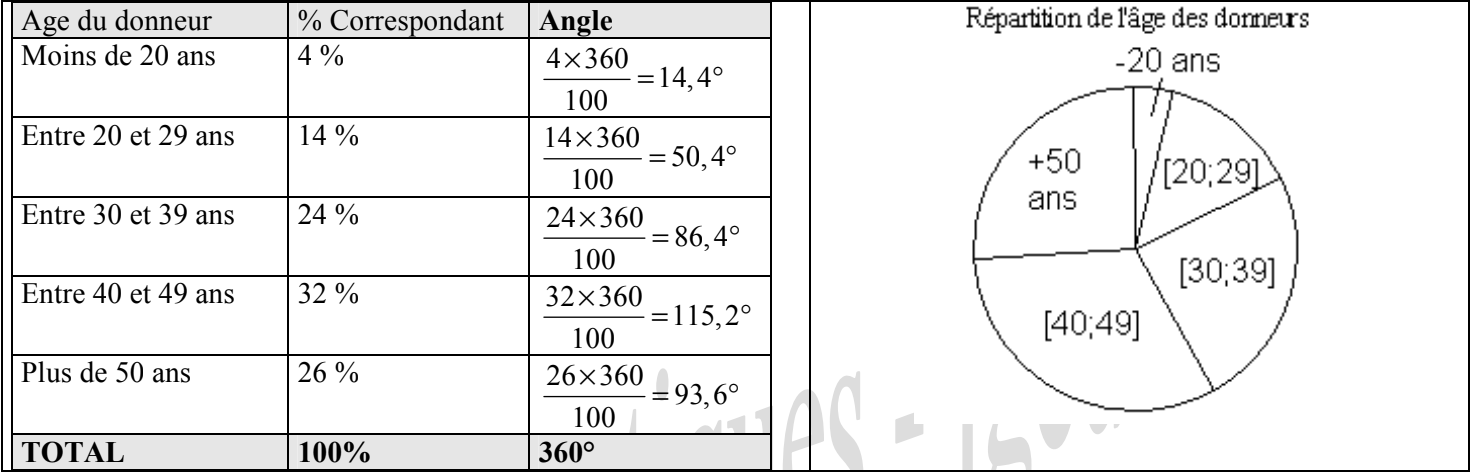
Représenter cette série statistique par un diagramme circulaire.
Exercice n°4.
Un élève a obtenu les notes suivantes : 4;6;3;9;10;8;12;10;19;12;20;12;18 . Calculer sa moyenne
Exercice n°5.
Un industriel a commandé à un sous-traitant un lot de 40 pièces dont le diamètre doit mesurer 80 mm et il est convenu que le lot ne sera accepté que si les deux conditions suivantes sont simultanément réalisées :
Première condition : l’écart entre 80 mm et la moyenne x du lot est inférieur à 0,05 mm
Deuxième condition : Au moins 60 % des pièces du lot ont un diamètre d tel que
80 − 0,05 ≤ ≤ 80 + 0,05 d (1)
Les mesures faites sur le lot sont les suivantes :
1) Calculer la moyenne x des mesures faites
2) Quel est le pourcentage de pièces dont le diamètre d vérifie la double inégalité (1) ?
3) Le lot est-il accepté ou refusé par l’industriel ? Justifier la réponse
Exercice n°6.
Un relevé des durées des communications téléphoniques effectués dans un central téléphonique a fourni les informations consignées dans le tableau suivant (l'unité de durée est la minute)
| Intervalle de durée | [0;2[ | [2;4[ | [4;6[ | [6;8[ | [8;10[ | [10;12[ |
| Effectif | 14 | 16 | 25 | 15 | 17 | 13 |
1) Calculer la durée moyenne d'un appel
2) On regroupe les classes par deux, ce qui revient à considérer les classes [0;4[, [4,8[ et [8;12[.Calculer la durée moyenne d'un appel pour cette nouvelle série
3) Quelle conclusion pouvez-vous formuler ?
Exercice n°7.
Après correction des copies, la moyenne à l’épreuve de mathématiques au baccalauréat est x = 8,4 .
1) Si le ministre de l’Education Nationale décide d’augmenter la note de chaque copie de 1,6 point, quelle sera la nouvelle moyenne nationale ?
2) Si le ministre de l’Education Nationale décide d’augmenter la note de chaque copie de 10%, quelle sera la nouvelle moyenne nationale ?
Correction TD n°1
Exercice n°1
Exercice n°2
On dresse un tableau de proportionnalité entre chaque fréquence et l’angle du secteur angulaire correspondant
Exercice n°4
La moyenne de l’élève est égale à = (4 + 6 + 3 + 9 + 10 + 8 + 12 + 10 + 19 + 12 + 20 + 12 + 18) / 13 = 11
Exercice n°5
1) La moyenne x des mesures faites vaut :
(1 × 79,75 + 2 × 79,80 +.......+ 1 × 80,15 + 1 × 80,2) / 40 = 3198,9 / 40 = 79,9725
2) Le nombre de pièces dont le diamètre d vérifie la double inégalité (1) est égal à 6+14+5=25, soit un pourcentage égal à (25/40) = 62,5%
3) L’écart entre la moyenne x et 80 mm étant égal à 80 - 79,9725 = 0,0275 < 0,05, et plus de 60 % des pièces ayant un diamètre d vérifiant la double inégalité (1), le lot sera accepté.
Exercice n°6
1) Pour calculer la moyenne de cette série statistique, on prend en compte le milieu des classes, à savoir :
| Intervalle de durée | [0;2[ | [2;4[ | [4;6[ | [6;8[ | [8;10[ | [10;12[ |
| Milieu des classes | 1 | 3 | 5 | 7 | 9 | 11 |
| Effectif | 14 | 16 | 25 | 15 | 17 | 13 |
La durée moyenne d’un appel vaut donc : (1 × 14 + 3 × 16 ....... 9 × 17 + 11 × 13) / 100 = 588 / 100 = 5,88 minutes, soit 5 minutes et
0,88 × 60 = 52,8 secondes. La durée moyenne d’un appel vaut donc 5 minutes, 52 secondes et 8 dixièmes
2) La nouvelle série statistique est donc
| Intervalle de durée | [0;4[ | [4;8[ | [8;12[ |
| Effectif | 14+16=30 | 25+15=40 | 17+13=30 |
Pour calculer la moyenne de cette série statistique, on prend en compte le milieu des classes, à savoir
| Intervalle de durée | [0;4[ | [4;8[ | [8;12[ |
| Milieu des classes | 2 | 6 | 10 |
| Effectif | 30 | 40 | 30 |
La durée moyenne d’un appel calculée à partir de cette série vaut donc :
(2 × 30 + 6 × 40 + 10 × 30)/100 = 600/100 = 6 minutes
3) Selon la manière de regrouper les communications téléphoniques (donc seulement la présentation de la série statistique !), les résultats peuvent être différents
Exercice n°7
Après correction des copies, la moyenne à l’épreuve de mathématiques au baccalauréat est x = 8,4 .
1) Si les valeurs de la série statistique sont toutes augmentées d’une même valeur, sans modifier les effectifs, alors la moyenne subit la même transformation. La nouvelle moyenne de l’épreuve sera donc égale à 8,4+1,6=10
2) Augmenter une quantité de 10% revient à la multiplier par 1,1 Si les valeurs de la série statistique sont toutes multipliées par une même valeur, sans modifier les effectifs, alors la moyenne subit la même transformation. La nouvelle moyenne de l’épreuve sera donc égale à 1,1 × 8,4 = 9,24
TD n°2
Exercice 1
Partant des relevés mensuels des ventes de l’article référencé MAMXRT dans une
grande surface C au cours d’une année, on souhaite calculer la variance de la série.
Sont demandés : moyenne arithmétique, variance, écart-type.
| Quantite vendues | 1 | 2 | 3 | 4 | 5 |
| Nombre de mois | 2 | 3 | 3 | 2 | 2 |
Q1 : la moyenne arithmétique est égale à :
a) 2,92
b) 3,26
c) 5,45
d) 1,89
e) Aucune de ces réponses n’est correcte.
Q2 : la variance est égale à :
a) 1,25
b) 2,36
c) 1,74
d) 3,25
e) Aucune de ces réponses n’est correcte.
Q3: l’écart-type est égale à :
a) 1,87
b) 3,25
c) 1,98
d) 1,32
e) Aucune de ces réponses n’est correcte
Exercice 2
Dans une petite localité, on a relevé de nombre de pièces par appartement. Sont
demandés : mode, moyenne arithmétique, étendue, variance, écart-type.
| nombre de pièces | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| nombre d'appartement | 48 | 72 | 96 | 64 | 39 | 25 | 3 |
Q4 : Le mode est égale à :
a) 3
b) 6
c) 5
d) 2
e) Aucune de ces réponses n’est correcte.
Q5 : la moyenne est égale à :
a) 4,26
b) 2,87
c) 3,17
d) 3,89
e) Aucune de ces réponses n’est correcte.
Q6 : l’étendu est égale à :
a) 8
b) 9
c) 2
d) 6
e) Aucune de ces réponses n’est correcte.
Q7 : la variance est égale à :
a) 2,15
b) 3,12
c) 15,3
d) 4,25
e) Aucune de ces réponses n’est correcte.
Q8 : l’écart-type
a) 2,15
b) 1,14
c) 1,46
d) 4,25
e) Aucune de ces réponses n’est correcte.
Exercice 3
Sur un échantillon de 10 ménages, on associe le revenu mensuel du ménage (x)
(évalué en Dirhams) et le nombre d'individus qui composent la famille (y) :

Q9 : La moyenne des valeurs de x :
a) 1023
b) 922
c) 846
d) 896
e) Aucune de ces réponses n’est correcte.
Q10 : La moyenne des valeurs de y :
a) 4,8
b) 1,3
c) 3,2
d) 3,5
e) Aucune de ces réponses n’est correcte.
Q 11: La Variance des valeurs de x :
a) 6855
b) 2568
c) 45135
d) 4897
e) Aucune de ces réponses n’est correcte.
Q12 : La Variance des valeurs de y :
a) 1,16
b) 2,02
c) 1,46
d) 3,26
e) Aucune de ces réponses n’est correcte.
Q13: La covariance des valeurs de x et de y :
a) 132,5
b) 142,7
c) 140,6
d) 150,2
e) Aucune de ces réponses n’est correcte.
Q14 : Le coefficient de corrélation linéaire : r(x,y)= :
a) 0,568
b) 0,236
c) 0,689
d) 0,623
e) Aucune de ces réponses n’est correcte
Correction TD n°2
- A
- C
- D
- A
- C
- D
- A
- C
- B
- C
- C
- A
- B
- D
Supports module statistique descriptive S1
Voir aussi
- Exercices d'analyse mathématiques S1



Enregistrer un commentaire